You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

Background

当然不是那个经典的《寄蒜几盒》。

Description

在平面直角坐标系中，有一个无限长管道，我们定义区域$\{(x,y)|L\le x\le R, y\in \mathbb{R}\}$为管道内。

如果我们想让一个二维小球（可视为半径为$r$的二维圆盘）在管道内从$y=+\infty$运动到$y=-\infty$，很显然，这个小球的直径$d$不能超过管径$R-L$，因为如果小球更大，就无法塞进管道了。

然而问题并没有这么简单，由于一些原因，管道内存在着$n$个钉子（可视为有坐标、无面积的点状障碍物）。这样一来，直径$d=R-L$的二维小球就无法在管道内从$y=+\infty$贯穿到$y=-\infty$了，要使得小球能够做这样的运动，就必须减小其直径。

例如，如果在$x=\frac{L+R}{2}$（$y$任意）处放置一个钉子，那么只有直径不超过$\frac{R-L}{2}$的小球能在管道内从$y=+\infty$贯穿到$y=-\infty$。

现在，给定管道的范围$L,R$，以及管道内$n$个钉子的位置$(x_i,y_i)$，你需要求出能够在管道内从$y=+\infty$贯穿到$y=-\infty$的最大二维小球的尺寸。

注意： “贯穿”并不意味着小球运动轨迹的$y$坐标单调，你将在第二个样例中看到这一点。

Format

Input

第一行三个整数$n,L,R$，其意义见题目描述。

接下来$n$行，每行两个整数$(x_i,y_i)$，表示每个钉子的笛卡尔坐标，其中一定有$L\le x_i\le R$。

其中，钉子的坐标未必两两不同，但是很显然，多个重合的钉子在处理这个问题时可以当作一个。

Output

输出一行一个整数，表示符合题意的最大的二维小球（圆盘）的面积与$\frac{4}{\pi}$的乘积，结果保留到整数。

Samples

10 0 10
1 1
2 1
3 2
4 2
5 3
6 3
7 4
8 4
9 5
9 6

2

16 1 7
2 1
3 1
4 1
5 1
5 2
5 3
5 4
5 5
3 3
3 4
3 5
3 6
3 7
4 7
5 7
6 7

4

Limitation

$0\le n\le 5000$

$-10^9\le L\le x_i\le R\le 10^9$

$-10^9\le y_i\le 10^9$

Explanation

样例1解释

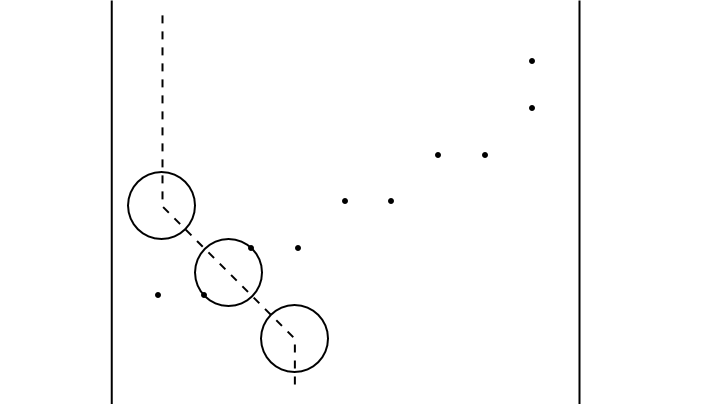
样例2解释

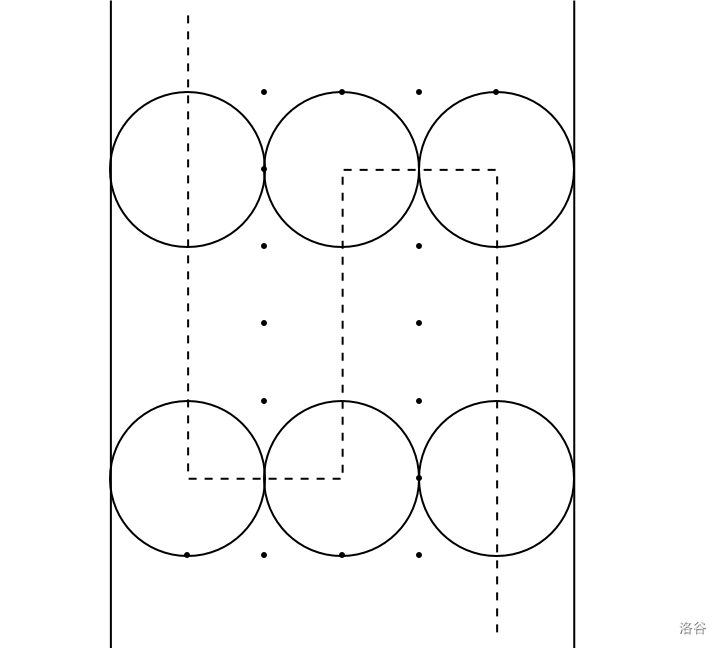
Tips

时限已放宽

请注意最后答案一定是整数，请考虑精度问题（建议不要用实数类型解决问题）

可以考虑把圆盘看成钉子，钉子看成圆盘，模型转化后再考虑 “小球无法贯穿” 的充要条件