scape
You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.
题目描述
暴走了!
暴走的 决定用自己的秘密武器把小 劈成两半。好消息是小 对 的武器提前有一定了解,他可以据此规划如何逃生。
具体来说,初始时小 和 两个人都视作位于 坐标系原点 的质点。约定小 开始逃跑的时刻为 。
小 已知 的武器由若干线段构成,但他不知道这些线段的具体形态,只知道所有线段端点都属于集合 ,其中 。
只能以 的角速度绕着 顺时针旋转这把武器,小 也只能以 的速度沿 轴正半轴逃跑。若某个 的时刻,小 与 武器上的任意一点(包括线段的端点)接触,小 就视为被武器击中而未能逃生。
经过交涉, 同意让小 先跑 秒(即 在 秒时开始旋转武器),但是如果 的值太大或者不是一个整数, 很可能会意识到自己被耍了,从而直接把小 扬了。
由于小 过于恐慌无法思考,请你帮助他求出最坏情况下,小 最少需要提前逃跑的整秒数 。
输入格式
第一行输入一个正整数 ,含义见题目描述。
接下来 行,每行输入两个整数 , ,描述点的坐标,保证任意两点不重合。
为了避免浮点数误差,数据保证小 最坏情况下提前逃跑恰好被击中的时间与 的差值大于 。
输出格式
一行,输出一个非负整数 ,表示最少需要提前逃跑的整秒数。
输入输出样例 #1
输入 #1
3
1 1
-1 1
0 4
输出 #1
0
输入输出样例 #2
输入 #2
5
-5 13
19 2
2 16
-7 16
17 12
输出 #2
14
说明/提示
下图展示了样例 中 武器的几种(并非全部)可能样式:
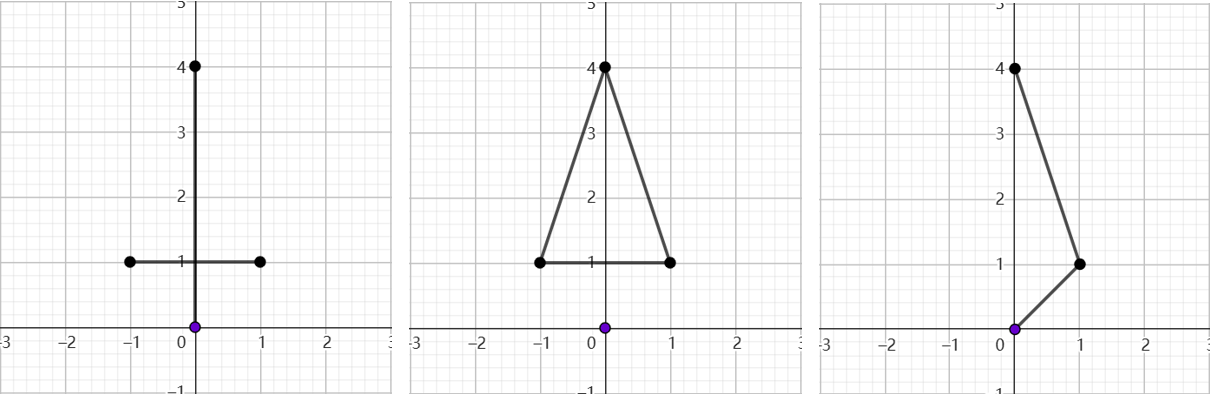
在以上三种情况下, 的武器提前旋转 秒才能击中小 。可以证明不存在更坏的情况,因此小 无需提前逃跑, .
中国科学院大学本科部第四届程序设计大赛(普及组)
- Status
- Done
- Rule
- ACM/ICPC
- Problem
- 7
- Start at
- 2025-5-24 13:30
- End at
- 2025-5-24 16:30
- Duration
- 3 hour(s)
- Host
- Partic.
- 24
