题目描述

小 $H$ 正在向 $Sanae$ 学习如何施法绘画五角星 $\text{*}$ 来进行星之仪式以召唤奇迹。

由于小 $H$ 法力较弱，$Sanae$ 为他规定了一个简单的任务。具体来说，设二人在一个二维平面 $xOy$ 内画星星，$Sanae$ 将会选定 $x$ 轴负半轴上一点 $A$ 以及第三象限内一点 $B$ ，且 $AB\parallel y$ 轴；此后 $Sanae$ 会另外选定平面内 $n$ 个可选的点 $(x_i,y_i)$ ，小 $H$ 只需要选出一对点 $(x_i,y_i)$ 和 $(x_j,y_j)$ ，顺次连接 $A-O-B-(x_i,y_i)-(x_j,y_j)-A$ 即可。

$Sanae$ 希望小 $H$ 画的五角星越多越好。由于小 $H$ 忙于练习施法，因此请你帮助他编程，求出总共有多少有序点对 $\{(x_i,y_i),(x_j,y_j)\}$ ，满足按上述要求进行连线能构成五角星。

$\text{*}$ 五角星定义为一个凸五边形全部 $5$ 条对角线构成的图案。

输入格式

第一行输入三个整数 $n,x_A,y_B\,(2\leq n\leq 2\times 10^5,-10^9\leq x_A,y_B < 0$ ，表示可选点的个数、$A$ 点的横坐标和 $B$ 点的纵坐标，即给定 $A(x_A,0),B(x_A,y_B)$ .

接下来 $n$ 行，每行输入两个整数 $x,y\,(-10^9\leq x,y\leq 10^9)$ ，描述一个可选点的坐标。

输出格式

输出一行一个整数，表示合法有序点对 $\{(x_i,y_i),(x_j,y_j)\}$ 的个数，判断条件见题面描述。

输入输出样例 #1

输入 #1

3 -4 -4
1 5
-2 2
0 -4

输出 #1

1

说明/提示

样例解释

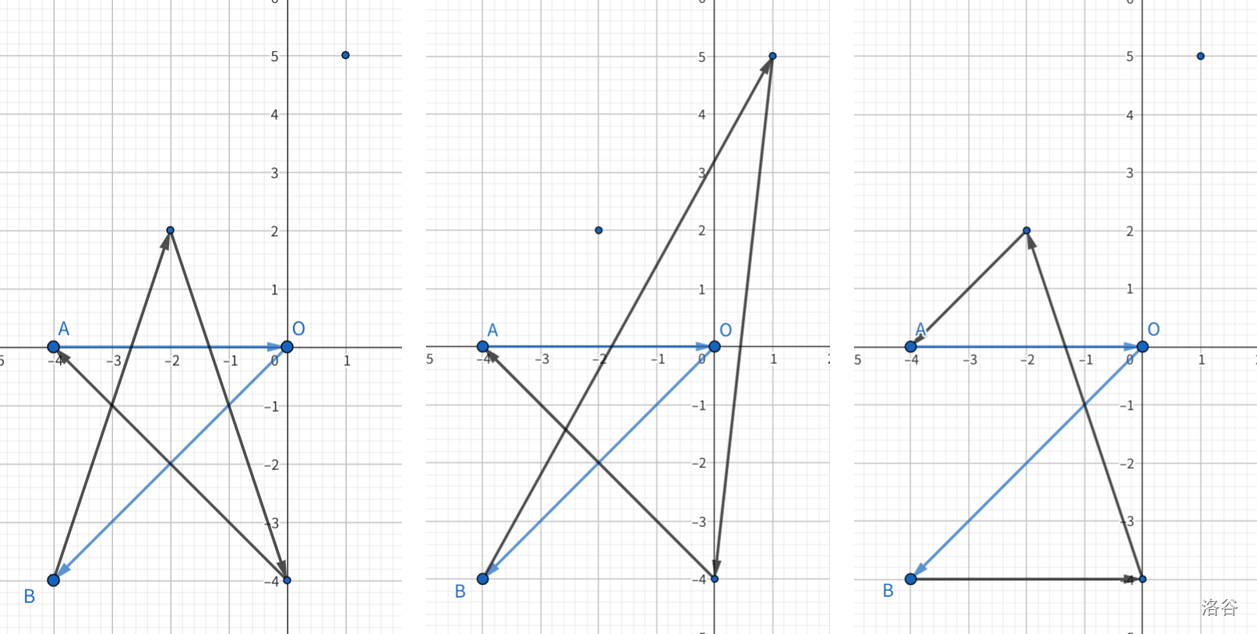
左侧图中展示了选择点对 $\{(x_2,y_2),(x_3,y_3)\}$ 时顺次连接 $A-O-B-(x_2,y_2)-(x_3,y_3)-A$ 构成的合法五角星图案。可以验证本样例中只有这种方案是合法的。

其余两张图展示了两种不合法的情形：中间图中选择点对 $\{(x_1,y_1),(x_3,y_3)\}$ 之后，$5$ 个点不能形成凸五边形；右侧图中选择点对 $\{(x_3,y_3),(x_2,y_2)\}$ 之后，虽然能构成凸五边形，但是顺次连接的 $5$ 条边不全是其对角线，因此图案也是非法的。